Disclaimer*

Disclaimer*

Much of the work I'll present is based off a fun idea

Disclaimer*

Much of the work I'll present is based off a fun idea

There ARE several major flaws, but this is primarily a proof of concept

Disclaimer*

Much of the work I'll present is based off a fun idea

There ARE several major flaws, but this is primarily a proof of concept

And I thought this would be more interesting than listening to me talk about LLM prompt engineering for 15 minutes

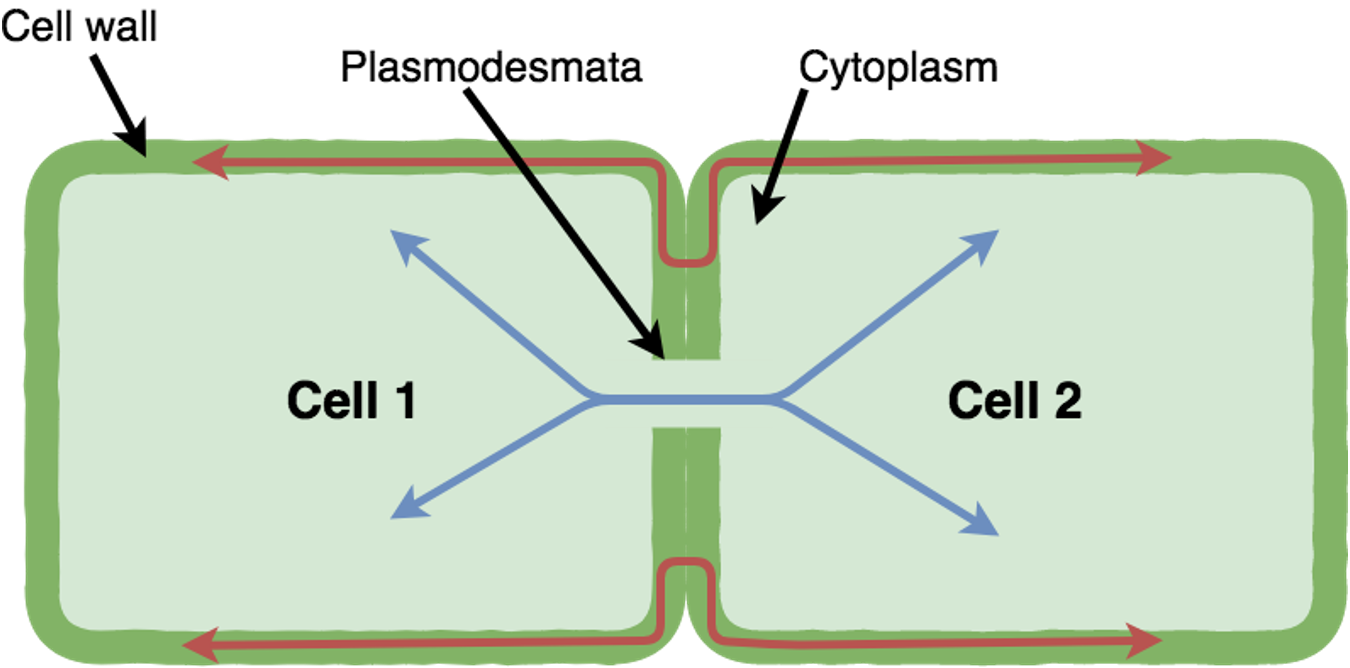
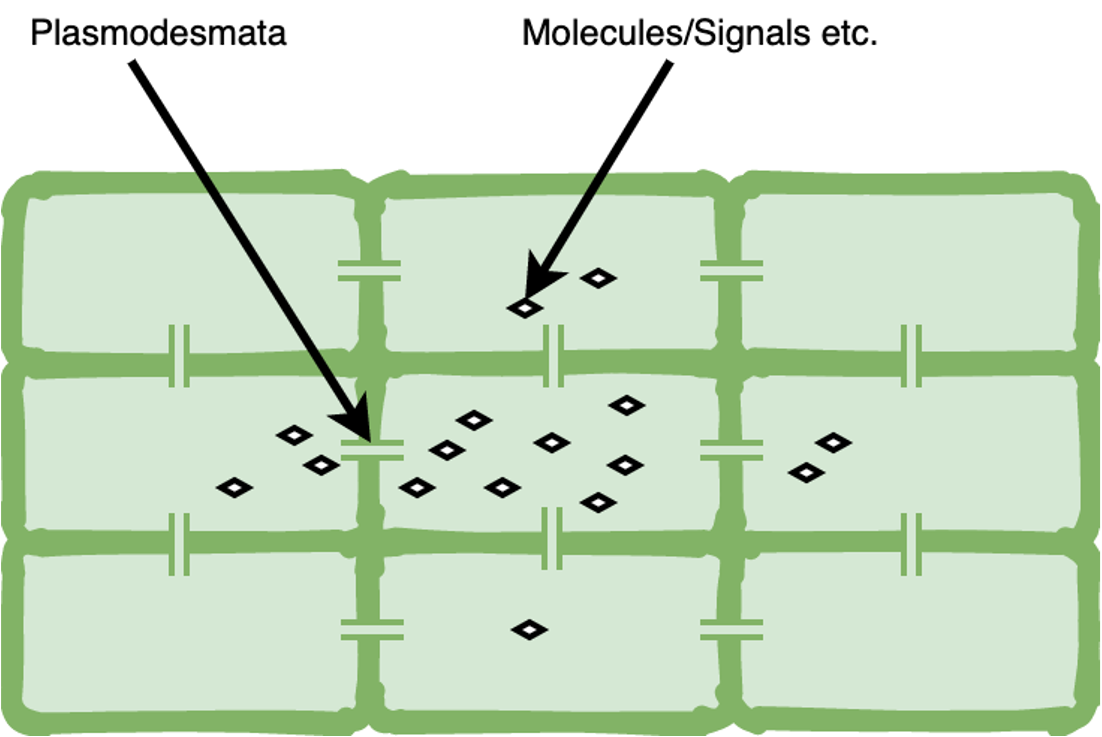
Plasmodesmata aren't just simple holes in the cell wall

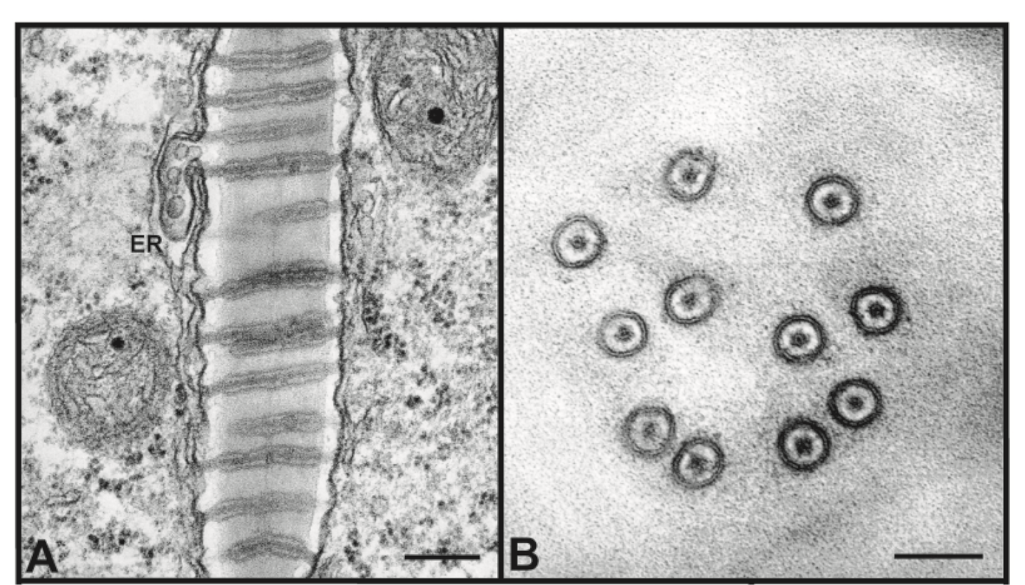
Image adapted from Plasmodesmata and the control of symplastic transport, Roberts 2003

How do molecules passively escape from cells?

Plasmodesmata seem to be a little 'random' in their placement

Plasmodesmata seem to be a little 'random' in their placement

Could their placement be better optimised?

Plasmodesmata seem to be a little 'random' in their placement

Could their placement be better optimised?

Does it need to be optimised?

H0: Evenly spacing PD decreases transport time

H0: Evenly spacing PD decreases transport time

H0: Evenly spacing PD decreases transport time

H0: Evenly spacing PD decreases transport time

Could some kind of optimization method find better or worse pore placements?

Genetic algorithms

Genetic algorithms

• Generate a population

Genetic algorithms

• Generate a population
• Evaluate fitness

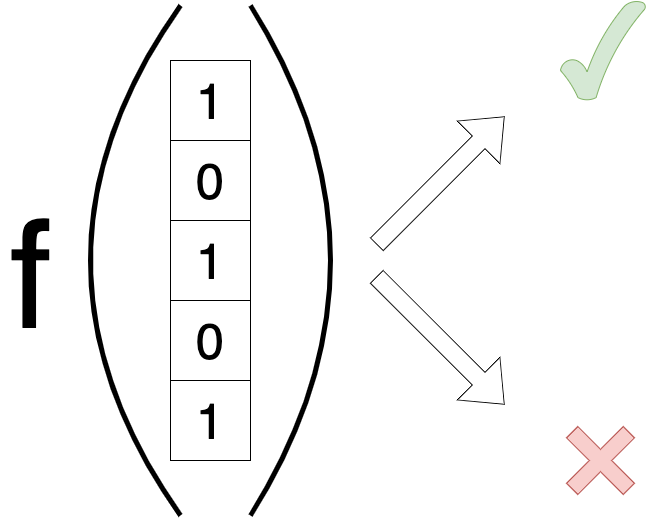
Genetic algorithms

• Generate a population
• Evaluate fitness
• Select parents

Genetic algorithms

• Generate a population
• Evaluate fitness
• Select parents
• Mating + mutations

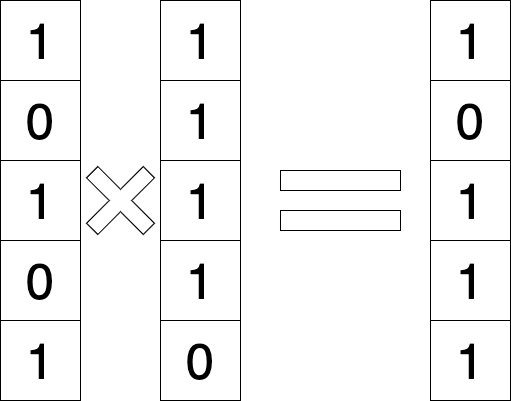
Genetic algorithms

• Generate a population
• Evaluate fitness
• Select parents
• Mating + mutations

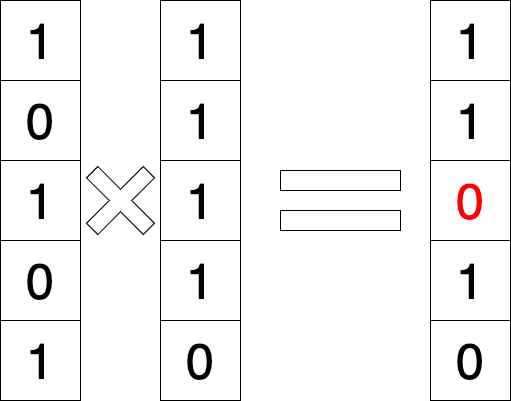
Genetic algorithms

• Generate a population
• Evaluate fitness
• Select parents
• Mating + mutations
• Repeat using offspring populaiton

Building a Plasmodesmata themed genetic algorithm

Generating a population

Evaluate best PD configurations using escape simulations

Evaluate best PD configurations using escape simulations

Parent selection

Parent 1

Parent 2

Create new generation (and repeat)

Parent 1

Parent 2

Offspring 1

Offspring 2

1. Generating a Random Population

def generate_random_pore_configs():
            return [np.array(points_on_cube_surface(pore_N, np.cbrt(v))) for _ in range(generation_size)]

This function creates an initial population of random pore configurations, essential for starting the genetic algorithm.

2. Mutation Function

def mutate(pores):
            mutations = np.random.random(len(pores))
            locs = np.where(mutations < mutation_rate)
            pores[locs] = np.array(points_on_cube_surface(len(locs), np.cbrt(v)))

Mutations introduce variations in the population, crucial for the evolution process in the genetic algorithm.

3. Fitness Evaluation

def evaluate_individual(pores):
            setups = [pores for _ in range(reps)]
            with multiprocessing.Pool(processes=os.cpu_count()) as pool:
                res = list(pool.imap(calc_escape_time, setups))
            return np.mean(res)

Evaluating the fitness of each individual in the population to determine their effectiveness in solving the problem.

4. Parent Selection

def choose_parents(times):
            return times.argsort()[:2]

Selecting the fittest individuals from the population to breed and produce the next generation.

5. Breeding and Creating New Generation

def breed(A, B):
    individuals = []
    for _ in range(generation_size):
        inherit = np.random.random(len(A))
        C = np.copy(A)
        locs = np.where(inherit < parent_inherit_divide)
        C[locs] = B[locs]
        individuals.append(C)
    return individuals

                    

This function combines the genetic information of two parents to create new offspring, introducing new variations.

6. The Main Genetic Algorithm Loop

                    for gen in tqdm(range(n_generations)):
                        fitness = evaluate_generation(cur_gen)
                        idA, idB = choose_parents(fitness)
                        for id, p in zip(['A','B'],[cur_gen[idA], cur_gen[idB]]):
                            t = np.mean(fitness[idA]) if id == 'A' else np.mean(fitness[idB]) 
                            if id == 'A':
                                print(f"Best time from generation {gen} is: {t}")
                            np.savetxt(f"./parents/pore_config_{gen}_{id}_{t}.csv", p)
                        new_gen = breed(cur_gen[idA], cur_gen[idB])
                        mutate_pop(new_gen)
                        # add randomness to pool to shake things up!
                        new_gen.append(generate_random_pore_configs()[0])
                        cur_gen = new_gen
                    

The main loop of the algorithm, where each generation is evaluated, parents are selected, offspring are created, and mutations are applied.

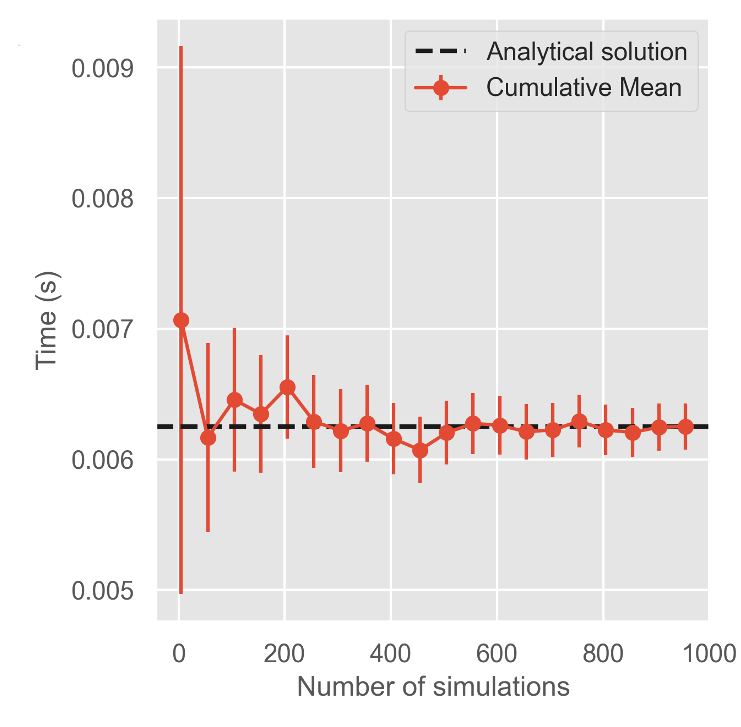
Can a genetic algorithm find an optimal PD arrangement?

Can a genetic algorithm find an optimal PD arrangement?

Can a genetic algorithm find an optimal PD arrangement?

Can a genetic algorithm find an optimal PD arrangement?

• Maybe...
• More experimentation needed!
• Perhaps change experimental setup dramatically
• Increase/Decrease mutation rates
• Run for a lot more generations
• Throw in a few "uniform" distributions to see if patterns are adopted
• Add sophistication in the mutations i.e. a "jitter" effect in their placement
• Genetic algorithms are well researched, and I am very naive, a lot of reading is needed on my end
• I should have used a library, but I wanted to use this as a learning experience

Thank you for your attention

Thank you for your attention

Any questions?