PyEscape - A narrow escape simulation library
What is the narrow escape problem


Escape time solution for a unit sphere with N pores
\[\begin{aligned} f(\epsilon) &= \epsilon - \frac{\epsilon^2}{\pi} \log \epsilon + \frac{\epsilon^2}{\pi} \log 2 \\ \sigma &= \frac{N \epsilon^2}{4} \\ \kappa(\sigma) &= \frac{4\sigma}{\pi - 4 \sqrt{\sigma}} \\ \tau &= \frac{f(\epsilon)}{3D\kappa(\sigma)} + (15D)^{-1} \end{aligned} \]
\[\begin{aligned} D = \textrm{Diffusion coefficient} \end{aligned} \] \[\begin{aligned} \epsilon = \textrm{Pore radii} \end{aligned} \] \[\begin{aligned} N = \textrm{Number of pores} \end{aligned} \]
Assumes uniformly distributed pores
Narrow-escape problem for the unit sphere: Homogenization limit, optimal arrangements of large numbers of traps, and the N2 conjecture. Cheviakov et al. 2013The simulation framework
- Written in Python 3
- Fully open source (MIT): https://github.com/AoifeHughes/NarrowEscapeSimulator
- Peer reviewed in Journal of Open Source Software: https://joss.theoj.org/papers/10.21105/joss.02072
- Published results in ieee journal: https://ieeexplore.ieee.org/document/9440948
The "escape" algorithm
- We use time step sizes of 1e-8 seconds
- Run 1000 simulations to get mean escape time
- For one experiment of 1 second real time: 100000000000 (100 billion) movement calculations
The "escape" algorithm
def escape(r, cur_pos, delta, pore_locs, pore_size, check_func, max_steps=1e10, tol=1, dt=1e-8):
pot_steps = fibonacci_spheres(max_steps, delta)
idx = 0
steps=0
while idx < len(pot_steps):
new_pos = cur_pos+pot_steps[idx]
while (not check_func(new_pos, r)) and idx < max_steps: # while not in container (invalid movement)
if passthrough_pore(new_pos, pore_locs, r=pore_size, tol=tol):
return (steps+1)*dt
idx += 1
new_pos = cur_pos+pot_steps[idx]
cur_pos = new_pos
steps+=1;idx+=1
return -1
def check_func(p, r):
return np.linalg.norm(p) < r
def passthrough_pore(p,p0, r=1, tol=1):
return np.any(np.linalg.norm(p-p0, axis=1) < r*tol)
More code examples
Multithreading and code reuse for multiple models:
from common_params import D, r, v, a, N, dt, MAX_steps, PS, ABCS
def esc(i):
p = i[1]
pores = fibonacci_spheres(p, v)
np.random.seed()
res, loc = escape(D, v, a, pores, dt=dt, tol=1, max_steps=MAX_steps, with_exit_loc=True)
return res, loc
if __name__ == "__main__":
idx = int(argv[1])
idy = 1
setups = {}
for p in PS:
for ABC in ABCS:
setups[idy] = (p, ABC)
idy += 1
try:
p, ABC = setups[idx]
except:
print('Setup not found... exiting')
exit()
# this change here is to make comparable to the cubeoid experiments
p = len(points_on_cuboid(np.array(ABC), vol=v, npts=p))
args = [[i, p] for i in np.arange(0,N)]
with multiprocessing.Pool(processes=os.cpu_count()) as pool:
res = list(tqdm.tqdm(pool.imap(esc, args), total=N))
res_t = [r[0] for r in res]
res_loc = [r[1] for r in res]
np.savetxt(f"./results/NEP_Sphere_{p}Pores_{N}Reps_{D}D_{v}V_{a}A_{dt}dt.csv", res_t)
np.savetxt(f"./exits/NEP_Sphere_{p}Pores_{N}Reps_{D}", res_loc)
Turning into a command line app:
def main():
parser = argparse.ArgumentParser()
parser.add_argument('-D', help='Diffusion coefficient')
parser.add_argument('-v', help='Container volume')
parser.add_argument('-a', help='Escape pore area size')
parser.add_argument(
'-s', help='Shape to escape (cube or sphere)', default='cube')
parser.add_argument('-p', help='Number of pores', default=1)
parser.add_argument(
'-N', help='Number of simulations to run', default=1)
parser.add_argument(
'-dt', help='Difference in time to use', default=3e-8)
parser.add_argument(
'--cpu', help='Number of cores to use', default=1)
parser.add_argument(
'-o', help='Output file', default="./results.csv")
args = parser.parse_args()
args = vars(args)
D, v, a, s, p, n, dt, cpu = float(args['D']), float(args['v']), float(
args['a']), str(args['s']), int(args['p']), int(args['N']), float(args['dt']), int(args['cpu'])
res, _ = run_simulations(D, v, a, s, p, n, dt, cpu)
print(np.mean(res))
np.savetxt(args['o'], np.array(res).flatten(), delimiter=',')
if __name__ == '__main__':
main()
Turning into a command line app:
$ ./pyescape -D 100 -v 1, -a 0.1 -p 10 -N 100 --cpu 8 -o data.csv
Analysis of data
To determine if the NEP solution was accurate in estimating escape time we build a series of random walk models
The NEP solutions show good agreement with our random walk models
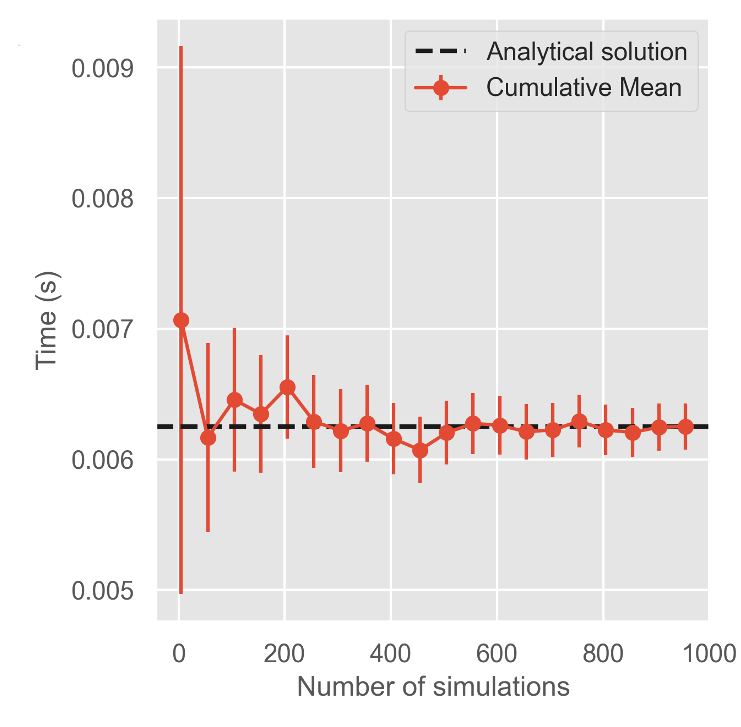
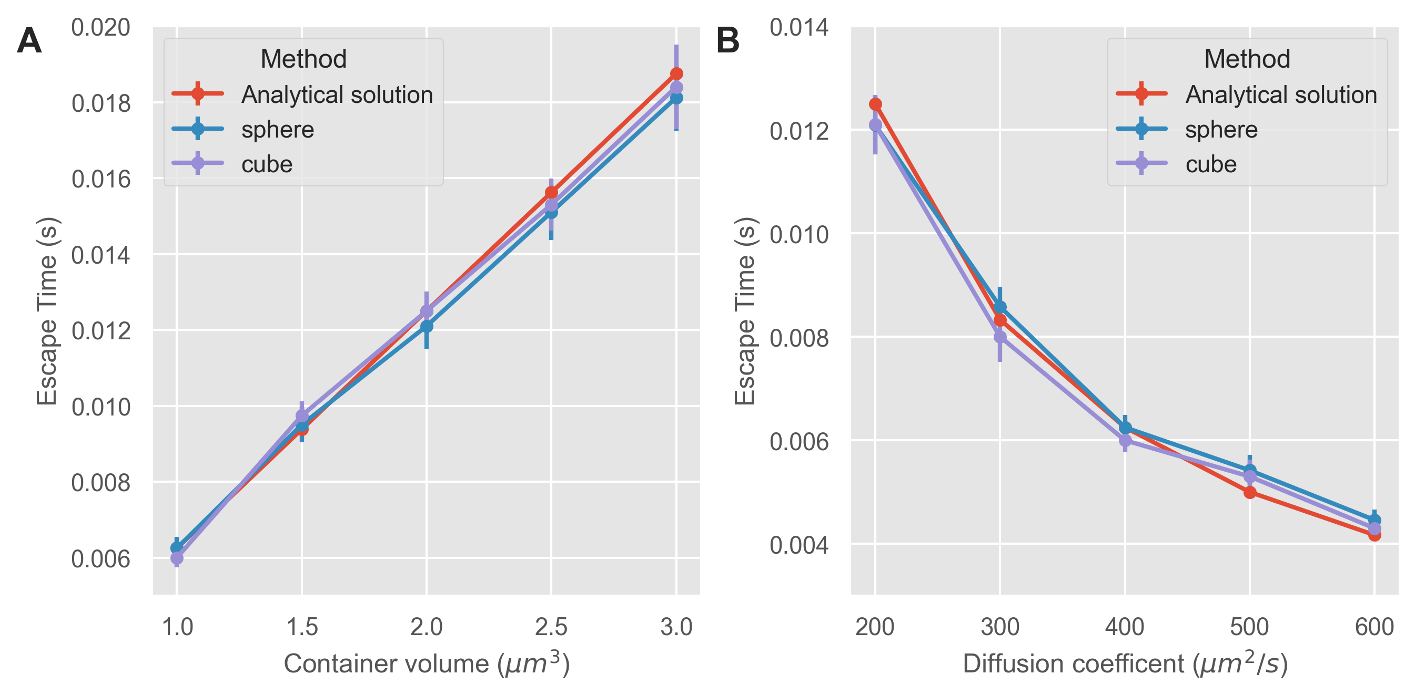
With other containers and parameters the NEP solutions show robustness in estimating the mean escape time
Narrow escape solutions deviate with asymmetric shapes
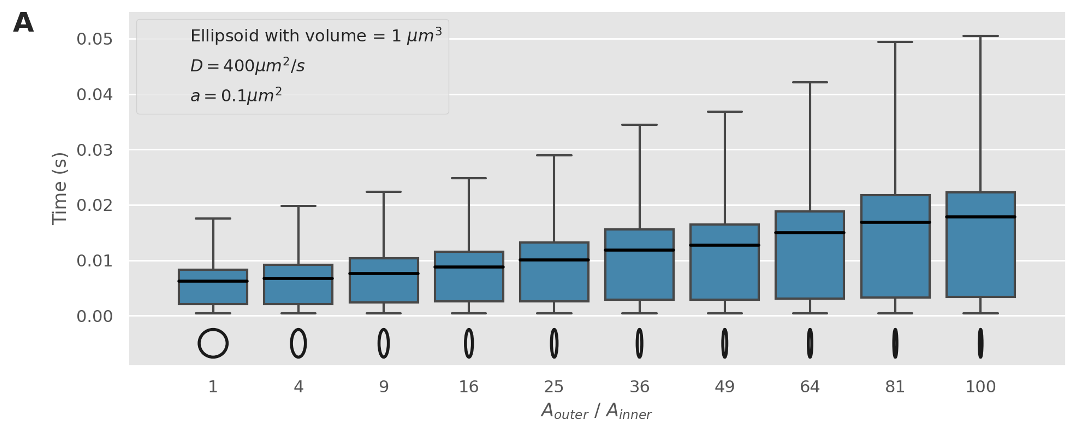
Narrow escape solutions deviate with asymmetric shapes
Adjusting the NEP solution to use a larger volume, we find that a correction factor can be applied to cope with these asymmetric shapes
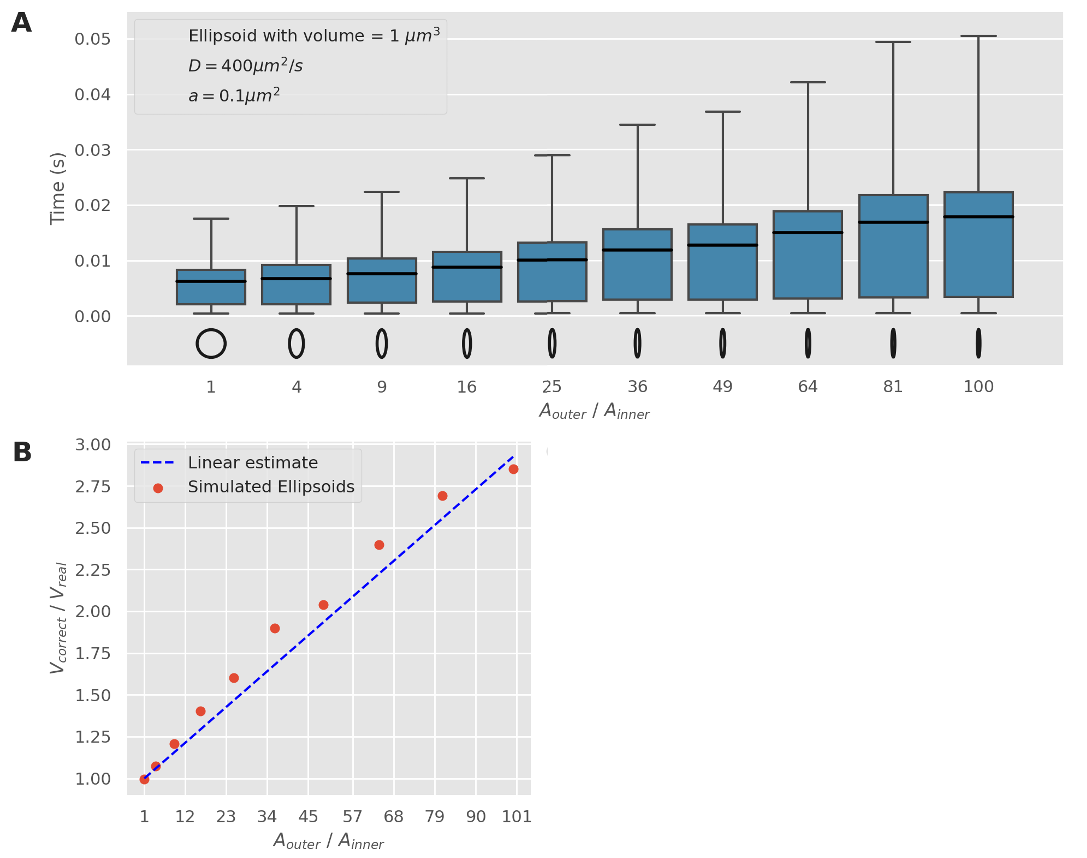
Narrow escape solutions deviate with asymmetric shapes
Adjusting the NEP solution to use a larger volume, we find that a correction factor can be applied to cope with these asymmetric shapes
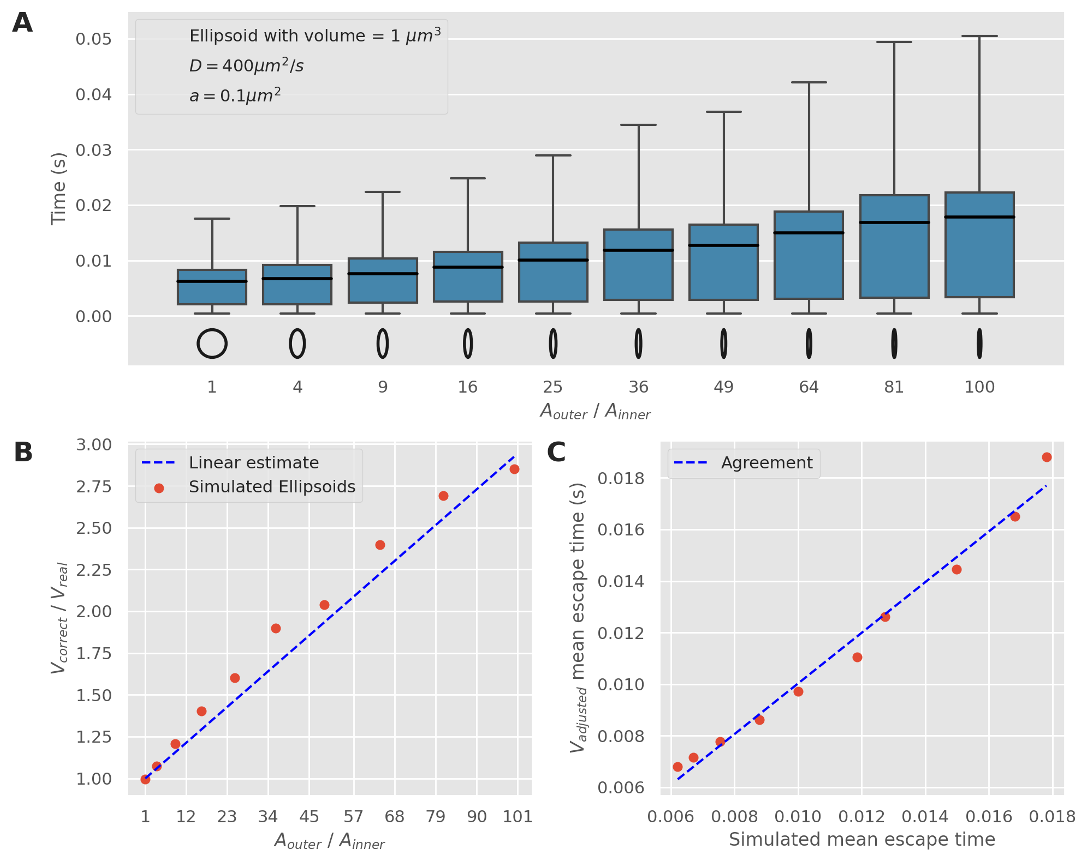
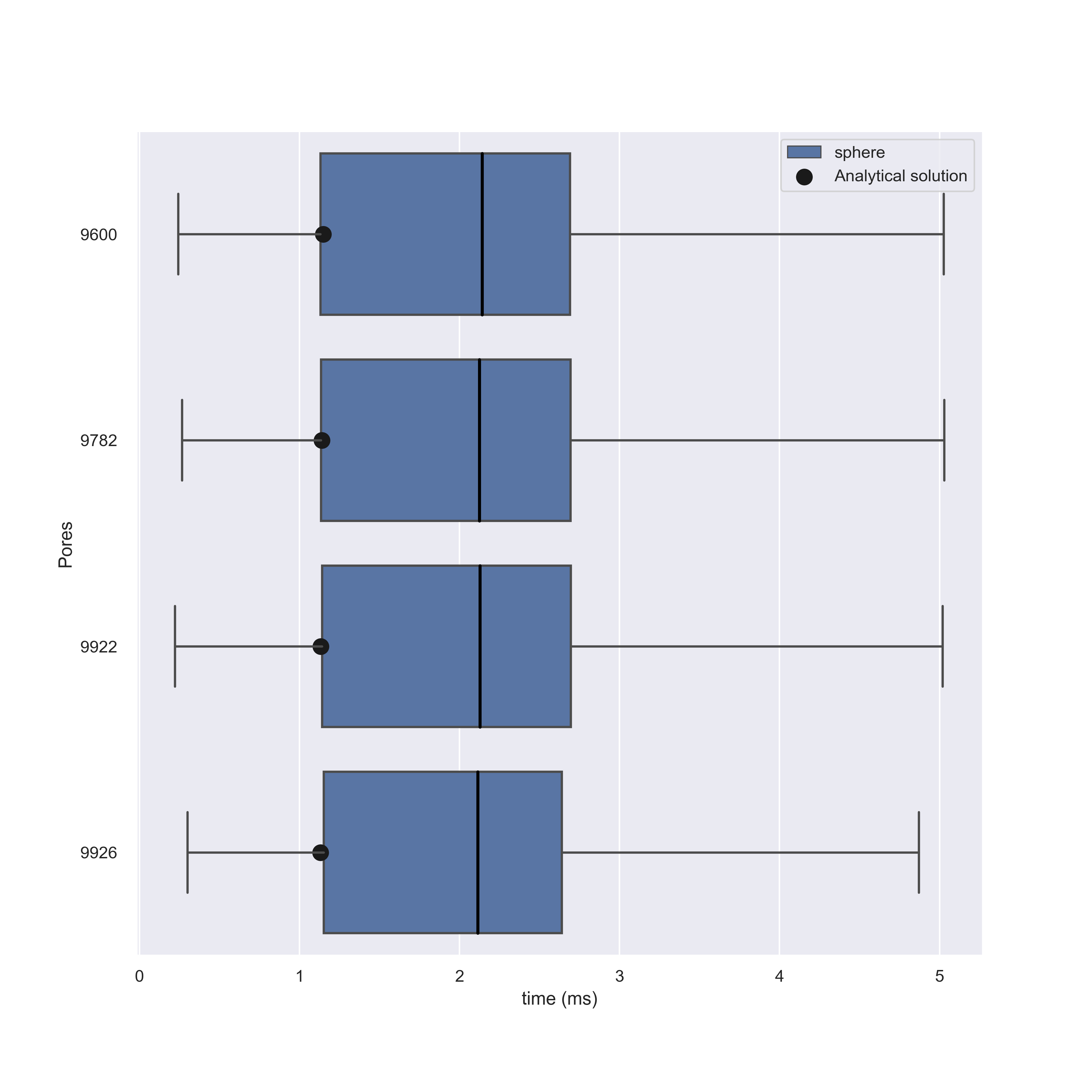
Running these simulations we find that NEP solutions are in agreement with our models, but for higher number of pores this begins to diminish
Running these simulations we find that NEP solutions are in agreement with our models, but for higher number of pores this begins to diminish
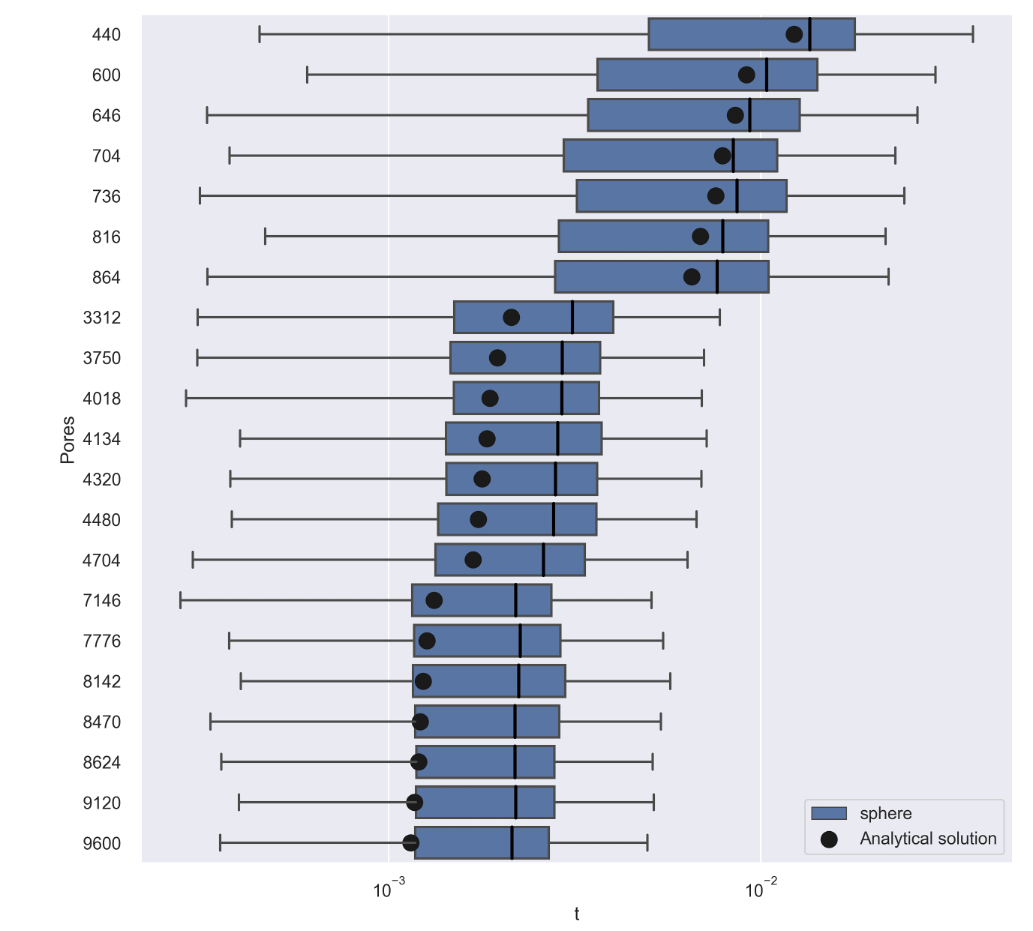
Running these simulations we find that NEP solutions are in agreement with our models, but for higher number of pores this begins to diminish
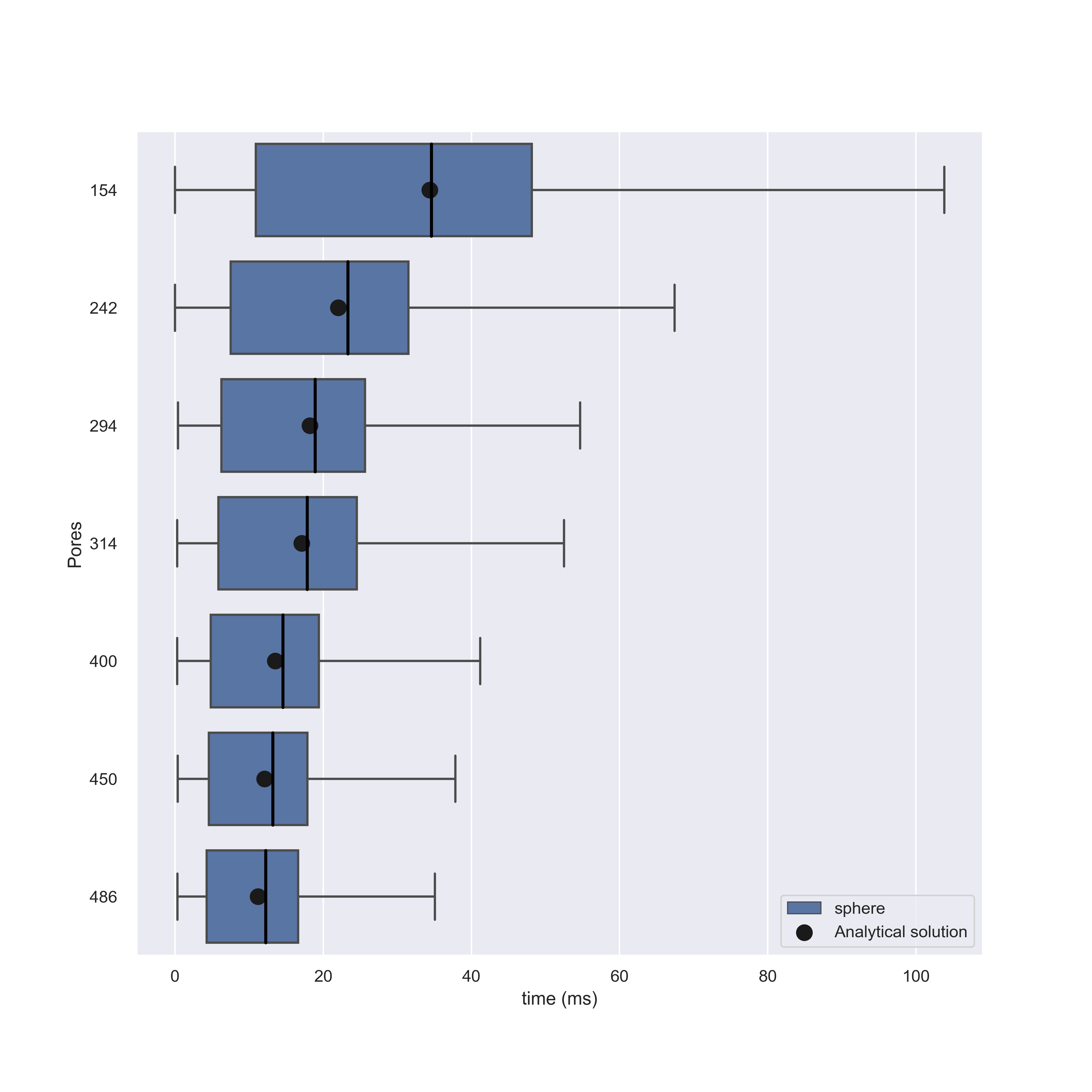
Running these simulations we find that NEP solutions are in agreement with our models, but for higher number of pores this begins to diminish

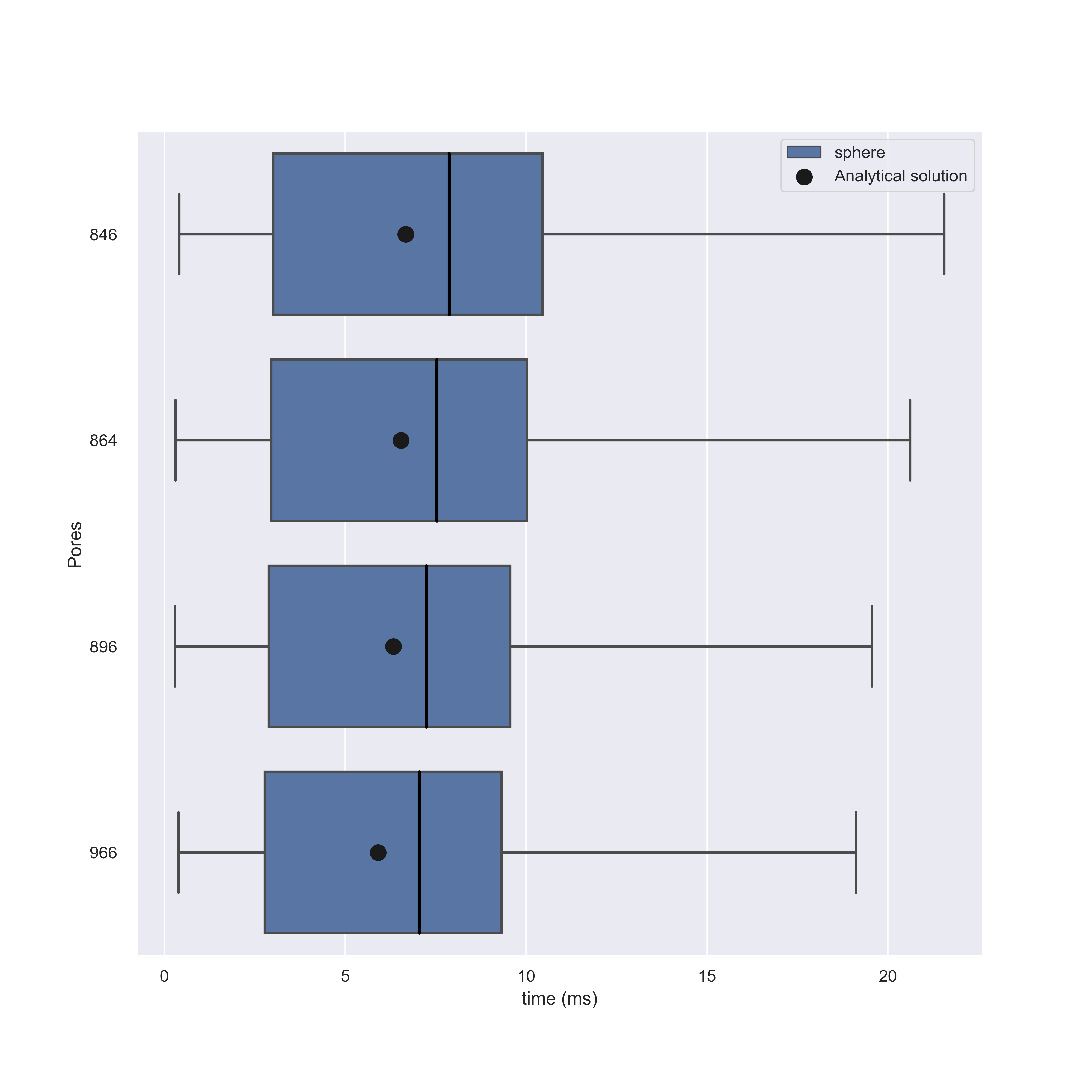
Running these simulations we find that NEP solutions are in agreement with our models, but for higher number of pores this begins to diminish


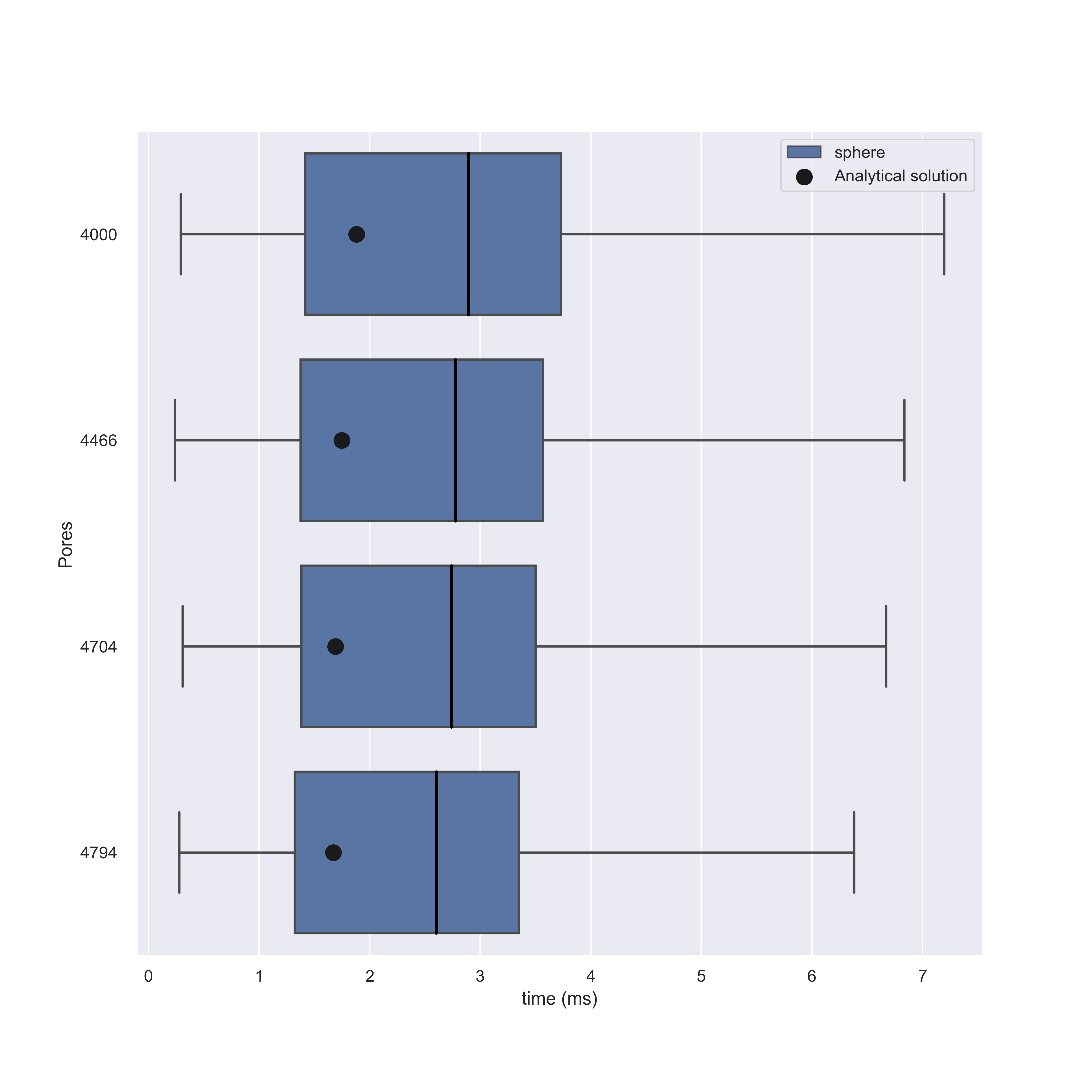
Running these simulations we find that NEP solutions are in agreement with our models, but for higher number of pores this begins to diminish